1.1 Parking Lot

New section content

The next example illustrates the algebraic technique of “multiplying by the conjugate,” which can be used to treat some indeterminate forms involving square roots.

Example 3 Multiplying by the Conjugate

Evaluate .

Solution We check that 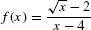has the indeterminate form 0/0 at x = 4:

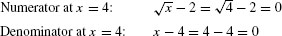
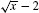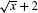Note, in Step 1, that the conjugate ofis, so.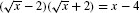

Step 1. Multiply by the conjugate and cancel.

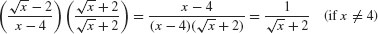
Step 2. Substitute (evaluate using continuity).

Because 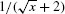is continuous at x = 4,

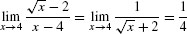
Example 4

Evaluate .

Solution We note that 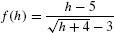yields 0/0 at h = 5:

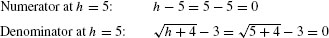
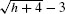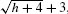The conjugate of is , and

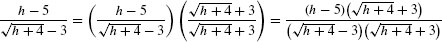
The denominator is equal to

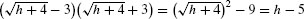
Thus, for h ≠ 5,

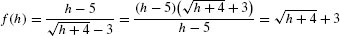
We obtain

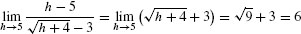
93

As preparation for the derivative in Chapter 3, we evaluate a limit involving a symbolic constant.

Example 7 Symbolic Constant

Calculate , where a is a constant.

Solution We have the indeterminate form 0/0 at h = 0 because

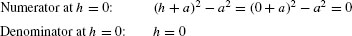
Expand the numerator and simplify (for h ≠ 0):

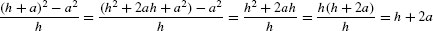
The function h + 2a is continuous (for any constant a), so

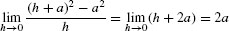
Figure 1.1: The earth’s average temperature (according to a simple climate model) in response to an 0.25% increase in solar radiation. According to this model, .

Example 1

Solution By definition, is a positive solution to the equation x^2=2. We set f(x) = x^2-2 and observe that f(1) =-1<0 and f(2)=2>0. Therefore, by Corollary 2, there exists a real number c in (1,2) such that c^2=2. Hence exists and is a real number.